Математика 9 класс: Геометрическая прогрессия

Геометри́ческая прогре́ссия — последовательность чисел

b_1,\ b_2,\ b_3,\ \ldots

(членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число

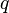q \quad

(знаменатель прогрессии), где

b_1\not=0

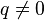q\not=0

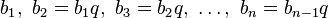b_1,\ b_2=b_1q,\ b_3=b_2q,\ \ldots,\ b_n=b_{n-1}q

Описание:

Любой член геометрической прогрессии может быть вычислен по формуле:

b_n=b_1q^{n-1} \quad

Если

b_1>0

q>1

, прогрессия является возрастающей последовательностью, если

0<q<1

, — убывающей последовательностью, а при

q<0

—знакочередующейся^[2].

Своё название прогрессия получила по своему характеристическому свойству:

|b_{n}| = \sqrt{b_{n-1} b_{n+1}},

то есть каждый член равен среднему геометрическому его соседей.

Примеры:

Последовательность площадей квадратов, где каждый следующий квадрат получается соединением середин сторон предыдущего — бесконечная геометрическая прогрессия со знаменателем 1/2. Площади получающихся на каждом шаге треугольников также образуют бесконечную геометрическую прогрессию со знаменателем 1/2, сумма которой равна площади начального квадрата^[3]^:8-9.

Последовательность количества зёрен на клетках в задаче о зёрнах на шахматной доске.
2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192 — прогрессия со знаменателем 2 из тринадцати членов.
50; −25; 12,5; −6,25; 3,125; … — бесконечно убывающая прогрессия со знаменателем -½.
$\pi, \pi, \pi, \pi$ — геометрическая прогрессия со знаменателем 1 (и арифметическая прогрессия с шагом 0).

Свойства:

$b_{n}^2 = b_{n-i} b_{n+i}$ , если $1 < i < n$ .
Произведение первых n членов геометрической прогрессии можно рассчитать по формуле:
$P_{n} = ( b_1 \cdot b_n )^\frac{n}{2}$ .
Произведение членов геометрической прогрессии начиная с k-ого члена, и заканчивая n-ым членом, можно рассчитать по формуле:
$P_{k,n} = \frac{ P_{n} }{ P_{k-1} }$ .
Сумма $n$ первых членов геометрической прогрессии:
$S_n = \begin{cases} \sum\limits_{i=1}^n b_i = \frac{ b_1 - b_1 q^{n} }{1-q}=\frac{ b_1 (1 - q^{n} ) }{ 1-q }, & \mbox{if } q \ne 1 \\ \\ n b_1, & \mbox{if } q = 1 \end{cases}$

Если $\left| q \right|<1$ , то $b_n \to 0$ при $n \to +\infty$ , и

$S_n \to {b_1 \over 1-q}$ при $n \to +\infty$ .