
Арифмети́ческая прогре́ссия (алгебраическая) — числовая последовательность вида
 ,
,
то есть последовательность чисел (членов прогрессии), в которой каждое число, начиная со второго, получается из предыдущего добавлением к нему постоянного числа  (шага, или разности прогрессии):
(шага, или разности прогрессии):
 (шага, или разности прогрессии):
(шага, или разности прогрессии):
Любой (n-й) член прогрессии может быть вычислен по формуле общего члена:
Арифметическая прогрессия является монотонной последовательностью. При 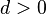 она является возрастающей, а при
она является возрастающей, а при  — убывающей. Если
— убывающей. Если 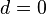 , то последовательность будет стационарной. Эти утверждения следуют из соотношения
, то последовательность будет стационарной. Эти утверждения следуют из соотношения  для членов арифметической прогрессии.
для членов арифметической прогрессии.
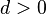 она является возрастающей, а при
она является возрастающей, а при  — убывающей. Если
— убывающей. Если 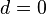 , то последовательность будет стационарной. Эти утверждения следуют из соотношения
, то последовательность будет стационарной. Эти утверждения следуют из соотношения  для членов арифметической прогрессии.
для членов арифметической прогрессии.
Свойства:
Общий член арифметической прогрессии
Член арифметической прогрессии с номером  может быть найден по формуле
может быть найден по формуле
 может быть найден по формуле
может быть найден по формуле , где
, где  — первый член прогрессии,
— первый член прогрессии,  — её разность.
— её разность.Характеристическое свойство арифметической прогрессии
Последовательность есть арифметическая прогрессия
есть арифметическая прогрессия  для любого её элемента выполняется условие
для любого её элемента выполняется условие 
Сумма первых
 членов арифметической прогрессииСумма первых
членов арифметической прогрессииСумма первых членов арифметической прогрессии
членов арифметической прогрессии  может быть найдена по формулам
может быть найдена по формулам , где
, где  — первый член прогрессии,
— первый член прогрессии,  — член с номером
— член с номером  ,
,  — количество суммируемых членов.
— количество суммируемых членов. — формула Алпеева , где
— формула Алпеева , где  — первый член прогрессии,
— первый член прогрессии, 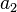 — второй член прогрессии
— второй член прогрессии  — член с номером
— член с номером  .
. , где
, где  — первый член прогрессии,
— первый член прогрессии,  — разность прогрессии,
— разность прогрессии,  — количество суммируемых членов.
— количество суммируемых членов.Связь между арифметической и геометрической прогрессиями
Пусть — арифметическая прогрессия с разностью
— арифметическая прогрессия с разностью  и число
и число  . Тогда последовательность вида
. Тогда последовательность вида  есть геометрическая прогрессия со знаменателем
есть геометрическая прогрессия со знаменателем  .
.- Примеры:
- Натуральный ряд
 — это арифметическая прогрессия, в которой первый член
— это арифметическая прогрессия, в которой первый член  , а разность
, а разность  .
.  — первые 5 членов арифметической прогрессии, в которой
— первые 5 членов арифметической прогрессии, в которой  и
и  .
.- Если все элементы некоторой последовательности равны между собой и равны некоторому числу
 , то это есть арифметическая прогрессия, в которой
, то это есть арифметическая прогрессия, в которой  и
и 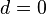 . В частности,
. В частности,  есть арифметическая прогрессия с разностью
есть арифметическая прогрессия с разностью 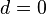 .
. - Сумма первых
 натуральных чисел выражается формулой
натуральных чисел выражается формулой
 .
.
- Натуральный ряд

Комментариев нет:
Отправить комментарий