Подобные треугольники — треугольники, углы которых соответственно равны, а стороны одного пропорциональны сходственным сторонам другого треугольника.
Признаки подобия треугольников
Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.
1-ый признак:
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.
|
то есть:

Дано:  и
и 
 и
и 
Доказать: 

Следствия первого признака подобия[править | править вики-текст]
- Если три разные стороны исходного треугольника попарно параллельны (дважды антипараллельны или перпендикулярны) трем разным сходственным сторонам другого треугольника, то указанные два треугольника с попарно параллельными (дважды антипараллельными или перпендикулярными) сторонами подобны. Примеры применения этого следствия см. ниже в разделах: "Примеры подобных треугольников" и "Свойства параллельности (антипараллельности) сторон родственных треугольников".
- Под дважды антипараллельными сторонами понимается следующее. Например, стороны данного остроугольного треугольника антипараллельны соответствующим сторонам ортотреугольника, против которых они лежат. В таком случае соответствующие стороны ортотреугольника ортотреугольника (дважды ортотреугольника) дважды антипараллельны соответствующим сторонам исходного треугольника, то есть просто параллельны. Следовательно, подобны, например,ортотреугольник ортотреугольника и исходный треугольник, как треугольники с параллельными сторонами.
Второй признак[править | править вики-текст]
Если угол одного треугольника равен углу другого треугольника, а стороны, образующие этот угол в одном треугольнике, пропорциональны соответствующим сторонам другого, то такие треугольники подобны.
|
Дано:  и
и  Доказать:
Доказать: 
 и
и  Доказать:
Доказать: 
Третий признак[править | править вики-текст]
Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого, то такие треугольники подобны.
|
Дано: ∆ABC и ∆A1B1C1,
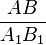 =
= 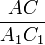 =
=  .
.
Доказать: ∆ABC 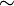 ∆A1B1C1.
∆A1B1C1.
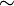 ∆A1B1C1.
∆A1B1C1.Признаки подобия прямоугольных треугольников[править | править вики-текст]
- По острому углу — см. первый признак;
- По двум катетам — см. второй признак;
- По катету и гипотенузе — см. третий признак.
Свойства подобных треугольников
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия
- Отношение объёма подобных стереометрических фигур равно кубу коэффициента подобия
- Отношение периметров и длин биссектрис, медиан, высот и серединных перпендикуляров равно коэффициенту подобия.
Примеры подобных треугольников
Подобных следующие виды треугольников:
- Дополнительный треугольник и антидополнительный треугольник подобны; соответственные их стороны параллельны.
- Данный треугольник ABC подобен своему дополнительному треугольнику; соответственные их стороны параллельны и относятся как 2:1.
- Данный треугольник ABC подобен своему антидополнительному треугольнику; соответственные их стороны параллельны и относятся как 1:2.
- Исходный треугольник
 по отношению к ортотреугольнику является треугольником трех внешних биссектрис[1].
по отношению к ортотреугольнику является треугольником трех внешних биссектрис[1]. - Ортотреугольник и тангенциальный треугольник подобны (Зетель, следствие 1, §66, с. 81).
- Ортотреугольник ортотреугольника и исходный треугольник подобны.
- Треугольник трёх внешних биссектрис треугольника трех внешних биссектрис и исходный треугольник подобны.
- Пусть, точки касания вписанной в данный треугольник окружности соединены отрезками, тогда получится треугольник Жергонна, и в полученном треугольнике проведены высоты. В этом случае прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника. Следовательно ортотреугольник треугольника Жергонна и исходный треугольник подобны.
- Выше указанные свойства подобия родственных треугольников являются следствием ниже перечисленных свойств параллельности сторон родственных треугольников.
- Теорема: окружностно-чевианный треугольник подобен подерному[2]. Здесь использованы определения:
- Треугольник с вершинами во вторых точках пересечения прямых, проведённых через вершины и данную точку, с описанной окружностью, называют окружностно-чевианным треугольником.
- Треугольник с вершинами в проекциях данной точки на стороны называется подерным или педальным треугольником этой точки.
Свойства параллельности (антипараллельности) сторон родственных треугольников:
- Соответственные стороны дополнительного треугольника, антидополнительного треугольника и исходного треугольника попарно параллельны.
- Стороны данного остроугольного треугольника антипараллельны соответствующим сторонам ортотреугольника, против которых они лежат.
- Стороны тангенциального треугольника антипараллельны соответствующим противоположным сторонам данного треугольника (по свойству антипараллельности касательных к окружности).
- Стороны тангенциального треугольника параллельны соответствующим сторонам ортотреугольника.
- Пусть, точки касания вписанной в данный треугольник окружности соединены отрезками, тогда получится треугольник Жергонна, и в полученном треугольнике проведены высоты. В этом случае прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника. Следовательно ортотреугольник треугольника Жергонна и исходный треугольник подобны.
Подобие в прямоугольном треугольнике
Треугольники, на которые высота, опущенная из прямого угла, делит прямоугольный треугольник, подобны всему треугольнику по первому признаку, а значит:
- Высота прямоугольного треугольника, опущенная на гипотенузу, равна среднему геометрическому проекций катетов на гипотенузу,
- Катет равен среднему геометрическому гипотенузы и проекции этого катета на гипотенузу.
Связанные определения
- Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников.
- Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов.

Комментариев нет:
Отправить комментарий